Example If V is the volume of the region Dbounded by the two surfaces z= x2 y2 and z= 2 x2 y2, then, changing to cylindrical coordinates, V = Z Z Z D dxdydz= Z 1 0 Z 2ˇ 0 Z 2 r2 r2 rdzd dr= Z 1 0 Z 2ˇ 0 2(r r3)d dr= ˇ;Write the equation in spherical coordinates 10 (a) z = x 2 y 2 (b) z = x 2 – y 2 Buy Find launch Calculus Early Transcendentals 8th Edition James Stewart Publisher Cengage Write the equation in spherical coordinates 10 (a) z = x 2 y 2 (b) z = x 2 – y 2 check_circle Expert Solution Want to see the full answer?Z 4 0 ˆ5 dˆ = ˇ Z 1 u=0 udu ˆ6 6 4 0!
1
X^2+y^2+z^2=16 in spherical coordinates
X^2+y^2+z^2=16 in spherical coordinates-Triple Integrals in Spherical Coordinates The spherical coordinates of a point M (x,y,z) are defined to be the three numbers ρ,φ,θ, where ρ is the length of the radius vector to the point M;Example # 4 Use Cylindrical or Spherical Coordinates to evaluate the integral −3 3 y − 9y−2 9y−2 x − 9x−2−y2 9x−2−y2 x2 y2 z2 z ⌠ ⎮ ⌡ d ⌠ ⎮ ⌡ d ⌠ ⎮ ⌡ d Page 8 of 18



2
Use spherical coordinates Evaluate ∭z dV, where E is between the spheres x ^ 2 y ^ 2 z ^ 2 = 16 and x ^ 2 y ^ 2 z ^ 2 = 25 in the first octantRectangular to Spherical Coordinate ConversionIf you enjoyed this video please consider liking, sharing, and subscribingYou can also help support my channelSpherical distance from (x;y;z) to the origin x 2 y 2 z = r Spherical coordinates parametrization of a sphere If ais a positive constant and a point (x;y;z) is on the sphere centered at the origin of radius a;then the coordinates satisfy the equation x2 y 2 z = a2 3
Where the evaluation of the nal double integral follows as in a previous example 232 Spherical coordinates A sphere that has Cartesian equation \(x^2y^2z^2=c^2\) has the simple equation \(ρ=c\) in spherical coordinates In geography, latitude and longitude are used to describe locations on Earth's surface, as shown in Figureφ is the angle between the projection of the radius vector −− → OM on the xy plane and the x axis;
The coordinate in the spherical coordinate system is the same as in the cylindrical coordinate system, so surfaces of the form are halfplanes, as before Last, consider surfaces of the form The points on these surfaces are at a fixed angle from the z axis and form a halfcone ( (Figure) ) In spherical coordinates we know that the equation of a sphere of radius \(a\) is given by, \\rho = a\ {x^2} {y^2} {z^2} = 16\ Now, if we substitute the equation for the cylinder into this equation we can find the value of \(z\) where the sphere and the cylinder intersectNote Remember that in polar coordinates dA = r dr d EX 1 Find the volume of the solid bounded above by the sphere x2 y2 z2 = 9, below by the plane z = 0 and laterally by the cylinder x2 y2 = 4 (Use cylindrical coordinates) θ Triple Integrals (Cylindrical and Spherical Coordinates) r
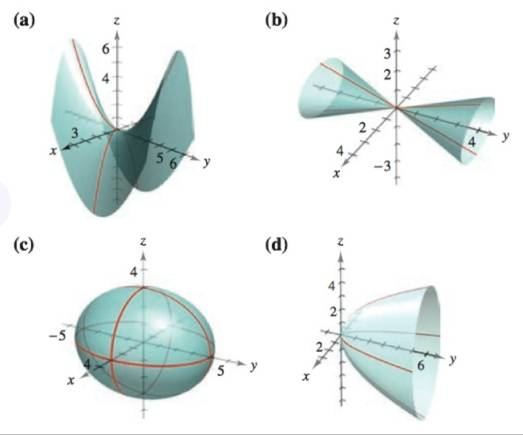



Matching In Exercises 5 10 Match The Equation With Its Graph The Graphs Are Labeled A B C D E And F X 2 9 Y 2 16 Z 2 9 1 Bartleby
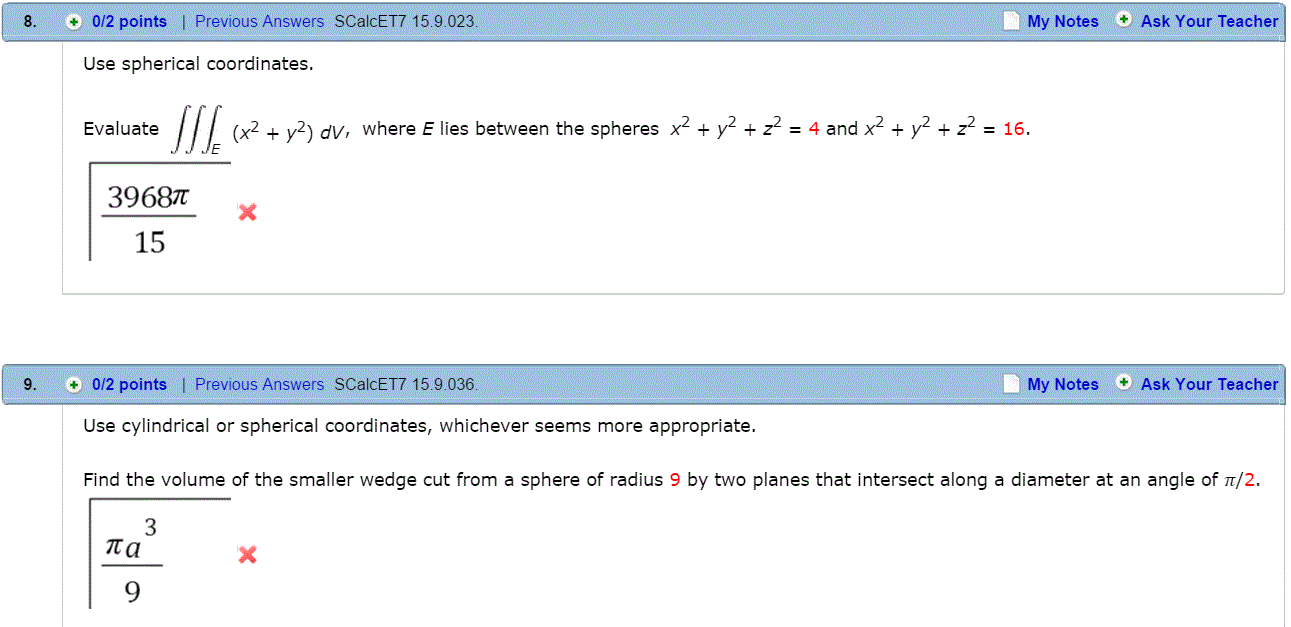



8 Use Spherical Coordinates Evaluate X2 Chegg Com
The lower bound z = x 2 y 2 z = x 2 y 2 is the upper half of a cone and the upper bound z = 18 − x 2 − y 2 z = 18 − x 2 − y 2 is the upper half of a sphere Therefore, we have 0 ≤ ρ ≤ 18, 0 ≤ ρ ≤ 18, which is 0 ≤ ρ ≤ 3 2 0 ≤ ρ ≤ 3 2 For the ranges of φ, φ, weShow transcribed image text Write the equation x^2 y^2 z^2 = 16 using cylindrical coordinates Use t in place of the Greek letter theta r^2 z^2 = 16 Now write the equation using spherical coordinates Use R for p, t for theta and F for phiConsider the surfaces x 2y z2 = 16 and x2 y2 = 4, shown below (a) Set up a triple integral in cylindrical coordinates which can be used to calculate the volume of the solid which is inside of x 2 yz 2 = 16 but outside of xy 2 = 4




Change In Variables Cylindrical Spherical Coordinates




Use Cylindrical Coordinates To Find The Volume Of The Solid Solid Inside Both X2 Y2 Z2 16 Homeworklib
6 (17 points) Evaluate the integral by changing to spherical coordinates Z 4 0 Zp 16 2y p 16 y2 Zp 16 x2 y2 0 (x2 y2 z2)zdzdxdy Solution Z 4 0 Zp 16 2y p 16 y2 Zp 16 x2 y2 0 (x 2y2 z 2)zdzdxdy= Z ˇ 0 Z ˇ=2 0 Z 4 0 ˆ ˆcos˚ˆ sin˚dˆd˚d = Z ˇ 0 d ˇ=2 0 sin˚cos˚d˚!The spherical shell bounded between x 2 y 2 z 2 = 16 and x 2 y 2 z 2 = 25 with density function δ (x, y, z) = x 2 y 2 z 2 39 The conical region bounded above z = x 2 y 2 and below the sphere x 2 y 2 z 2 = 1 with density function δ ( x , y , z ) = z So, given a point in spherical coordinates the cylindrical coordinates of the point will be, r = ρsinφ θ = θ z = ρcosφ r = ρ sin φ θ = θ z = ρ cos φ Note as well from the Pythagorean theorem we also get, ρ2 = r2 z2 ρ 2 = r 2 z 2 Next, let's find the Cartesian coordinates of the same point




4 Evaluate The Integral By Changing To Spherical Coordinates 15 8 41 43 X2 Y2 Homeworklib



Converting Equations From Polar To Rectangular Precalculus Socratic
Answer to Convert the following into spherical coordinates x^2 y^2 z^2 = 36 By signing up, you'll get thousands of stepbystep solutions toWrite the equation in spherical coordinates (a) x2 y2 z2 = 16 (b) x2 − y2 − z2 = 1 Question Write the equation in spherical coordinatesThe azimuthal angle is denoted by , it is the angle between the xaxis and




4 Evaluate The Integral By Changing To Spherical Coordinates 15 8 41 43 X2 Y2 Homeworklib




Polar Coordinates
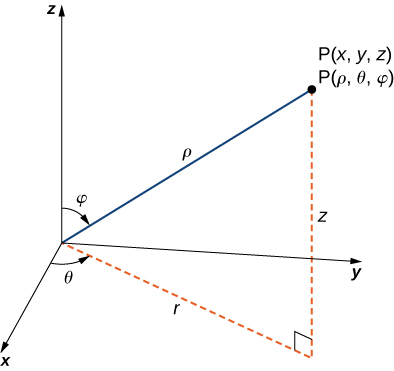
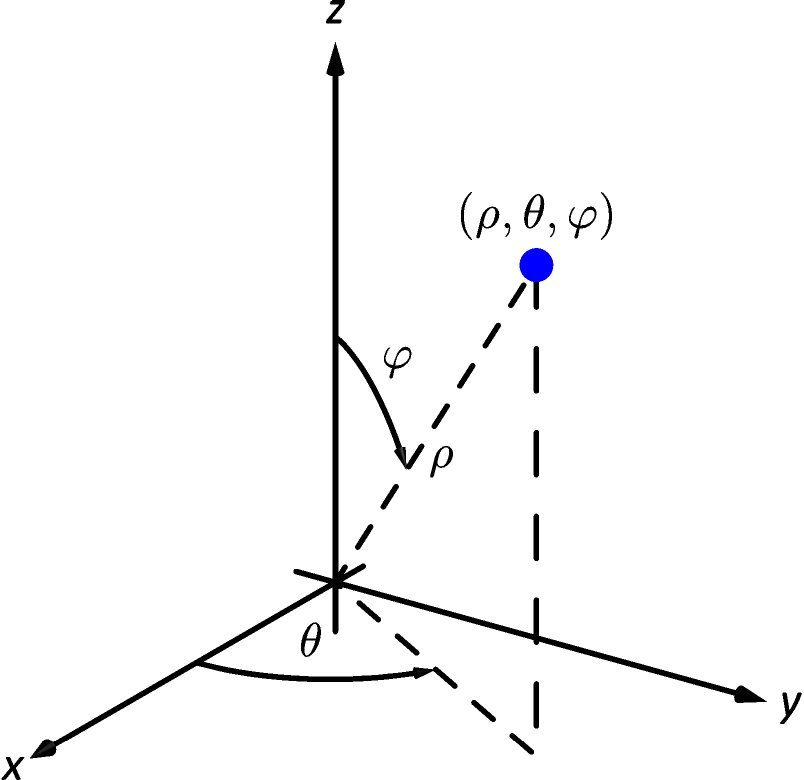
Notes This article uses the standard notation ISO , which supersedes ISO 3111, for spherical coordinates (other sources may reverse the definitions of θ and φ) The polar angle is denoted by , it is the angle between the zaxis and the radial vector connecting the origin to the point in question; Example 1586 Setting up a Triple Integral in Spherical Coordinates Set up an integral for the volume of the region bounded by the cone z = √3(x2 y2) and the hemisphere z = √4 − x2 − y2 (see the figure below) Figure 15 A region bounded below by a cone and above by a hemisphere SolutionWrite the equation in spherical coordinates (a) x2 y2 z2 = 16 (b) x2 − y2 − z2 = 1 Expert Answer 100% (26 ratings) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator



1




Evaluate The Volume Of The Solid Bounded By Z 8 X 2 Y 2 Z X 2 Y 2 X 1 Y Sqrt 3 X Y 0 Mathematics Stack Exchange
This spherical coordinates converter/calculator converts the rectangular (or cartesian) coordinates of a unit to its equivalent value in spherical coordinates, according to the formulas shown above Rectangular coordinates are depicted by 3 values, (X, Y, Z) When converted into spherical coordinates, the new values will be depicted as (r, θ, φ)This video explains how to set up a triple integral using spherical coordinates and then evaluate the triple integralhttp//mathispower4ucomA sphere that has the Cartesian equation x 2 y 2 z 2 = c 2 has the simple equation r = c in spherical coordinates Two important partial differential equations that arise in many physical problems, Laplace's equation and the Helmholtz equation, allow a separation of variables in spherical coordinates




Use Cylindrical Coordinates To Find The Volume Of The Solid Solid Inside Both X2 Y2 Z2 16 Homeworklib




Notes Up To Ch7 Sec3
Section 47 Triple Integrals in Spherical Coordinates Evaluate ∭ E 10xz 3dV ∭ E 10 x z 3 d V where E E is the region portion of x2 y2 z2 =16 x 2 y 2 z 2 = 16 with z ≥ 0 z ≥ 0 Solution Evaluate ∭ E x2y2dV ∭ E x 2 y 2 d V where E E is the region portion of x2 y2 z2 = 4 x 2 y 2 z 2 = 4 with y ≥ 0 y ≥ 0 Solutionθ is the angle of deviation of theSpherical coordinates determine the position of a point in threedimensional space based on the distance ρ from the origin and two angles θ and ϕ If one is familiar with polar coordinates, then the angle θ isn't too difficult to understand as it is essentially the same as the angle θ from polar coordinates



15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts



Triple Integrals In Cylindrical And Spherical Coordinates Calculus Volume 3
= ˇ u2 2 1 0!Cylindrical Coordinates x = r cosθ r = √x2 y2 y = r sinθ tan θ = y/x z = z z = z Spherical Coordinates x2 y2 z2 = 1 to spherical coordinates c) ρ = 2cos φ to cylindrical coordinates 8 EX 4 Make the required change in the given equation (continued)Section 26 Cylindrical and Spherical Coordinates A) Review on the Polar Coordinates The polar coordinate system consists of the origin O;the rotating ray or half line from O with unit tick A point P in the plane can be uniquely x2y 2z =2y or x2(y¡1)2z2=1 This is the sphere centered at (0;1;0)with radius R =1



Solved Consider The Solid That Is Bounded By The Cone Z 3 X 2 3 Y 2 And Above By The Sphere X 2 Y 2 Z 2 16 Set Up Only The Appropriate Tripl Course Hero




Triple Integrals And Volume Using Spherical Coordinates Youtube
Example Find the volume of the solid region above the cone z2 = 3(x2 y2) (z ≥ 0) and below the sphere x 2 y 2 z 2 = 4 Soln The sphere x 2 y 2 z 2 = 4 in spherical coordinates is ρ = 2The concept of triple integration in spherical coordinates can be extended to integration over a general solid, using the projections onto the coordinate planes Note that and mean the increments in volume and area, respectively The variables and are used as the variables for integration to express the integrals Section 47 Triple Integrals in Spherical Coordinates Evaluate ∭ E 4y2dV ∭ E 4 y 2 d V where E E is the sphere x2 y2 z2 =9 x 2 y 2 z 2 = 9 Evaluate ∭ E 3x−2ydV ∭ E 3 x − 2 y d V where E E is the region between the spheres x2 y2z2 = 1 x 2 y 2 z 2 = 1 and x2 y2 z2 =4 x 2 y 2 z 2 = 4 with z ≤ 0 z ≤ 0
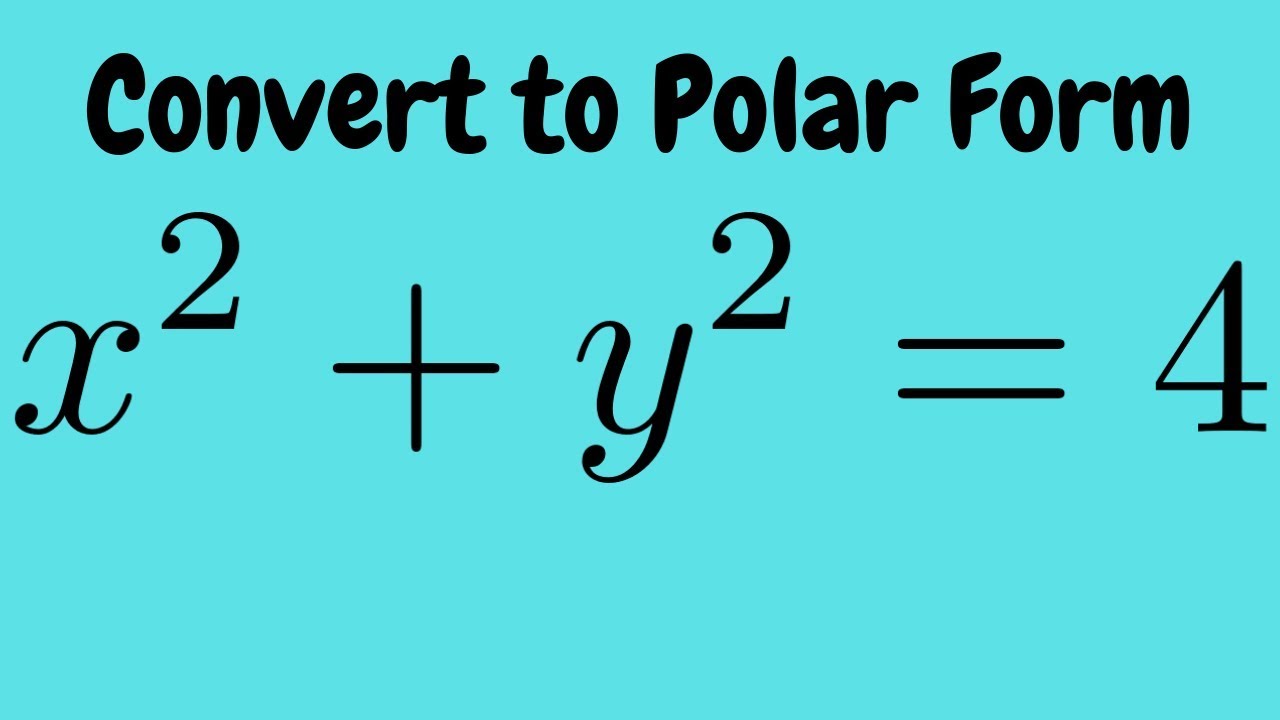



Converting The Rectangular Equation X 2 Y 2 4 Into Polar Form Youtube
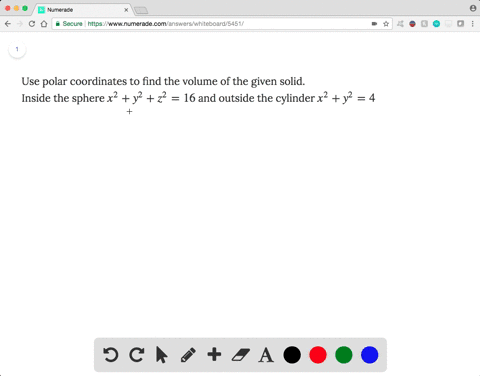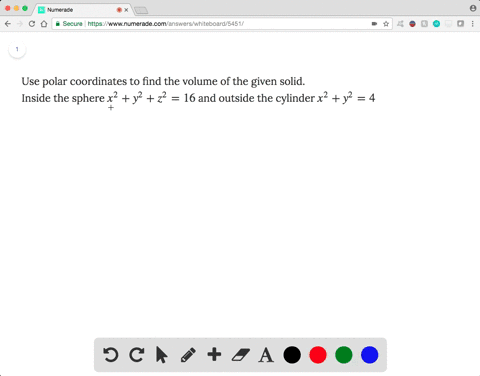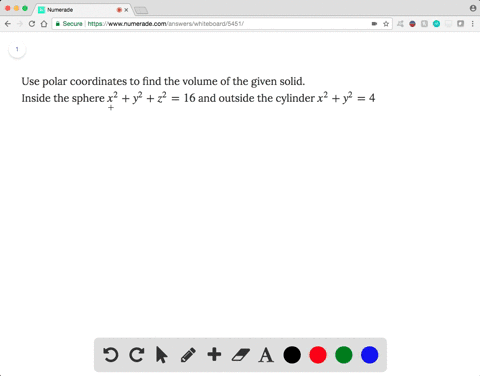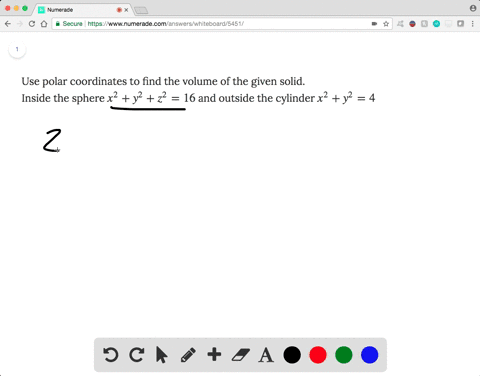



Solved Use Polar Coordinates To Find The Volume O
Find stepbystep solutions and your answer to the following textbook question Use spherical coordinates Evaluate triple integral (x^2y^2)dV, where E lies between the spheres x^2y^2z^2=4 and x^2y^2z^2=9 3 This is equation of a sphere, so you can write immediately that R 2 = 49, since x 2 y 2 z 2 = R 2 But you could get to this the way you started, simply by repeatedly using cos 2 x sin 2 x = 1 to simplify your final expression First, we need to recall just how spherical coordinates are defined The following sketch shows the relationship between the Cartesian and spherical coordinate systems Here are the conversion formulas for spherical coordinates x = ρsinφcosθ y = ρsinφsinθ z = ρcosφ x2y2z2 = ρ2 x = ρ sin



2




Find The Area Of The Surface The Part Of The Sphere X 2 Y 2 Z 2 A 2 That Lies Within The Cylinder X 2 Y 2 Ax And Above The Xy Plane Study Com
X 2 y2 is the same as ˚= ˇ 4 in spherical coordinates (1) The sphere x2y2z = 1 is ˆ= 1 in spherical coordinates So, the solid can be described in spherical coordinates as 0 ˆ 1, 0 ˚ ˇ 4, 0 2ˇ This means that the iterated integral is Z 2ˇ 0 Z ˇ=4 0 Z 1 0 (ˆcos˚)ˆ2 sin˚dˆd˚dQuestion Consider The Sphere X^2 Y^2 Z^2 = 16 (a) Use Spherical Coordinates To Parametric The Sphere (b) Let R Vector Be The Radius Vector Of The Sphere Compute Partial Differential R Vector/partial Differential Phi Times Partial Differential R Vector/partial Differential Theta (c) Find An Equation Of The Tangent Plane To The Sphere At The Point WhereAnswer to Find the volume of the solid that lies within the sphere x^2 y^2 z^2 = 1, above the xy plane, and outside the cone z = 4\sqrt{(x^2




Use Spherical Coordinates Evaluate 4 X2 Y2 Dv Where H Is The Solid Hemisphere Homeworklib



2
Spherical form r=cos phi csc^2 theta Cylindrical form r=z csc^2theta The conversion formulas, Cartesian to spherical (x, y, z)=r(sin phi cos theta, sin phi sin theta, cos phi), r=sqrt(x^2y^2z^2) Cartesian to cylindrical (x, y, z)=(rho cos theta, rho sin theta, z), rho=sqrt(x^2y^2) Substitutions in x^2y^2=z lead to the forms in the answer Note the nuancesUsing Spherical Coordinates Let P(x,y,z) be any point in the plane, then 1 {eq}\rho {/eq} is the distance between P and origin 2 {eq}\theta {/eq} is the same angle used to describe theAnswer to Use spherical coordinates to find the volume of solid within the sphere x^2 y^2 z^2 = 16 and above the cone 3z^2 = x^2 y^2 and



2



17 6 Cylindrical And Spherical Coordinates



2




1 Point Find The Volume Of The Solid That Lies Within The Sphere X2 2 Z 64 Above The Xy Plane And Outside The Cone Z 8v X2 Y2 1 Point
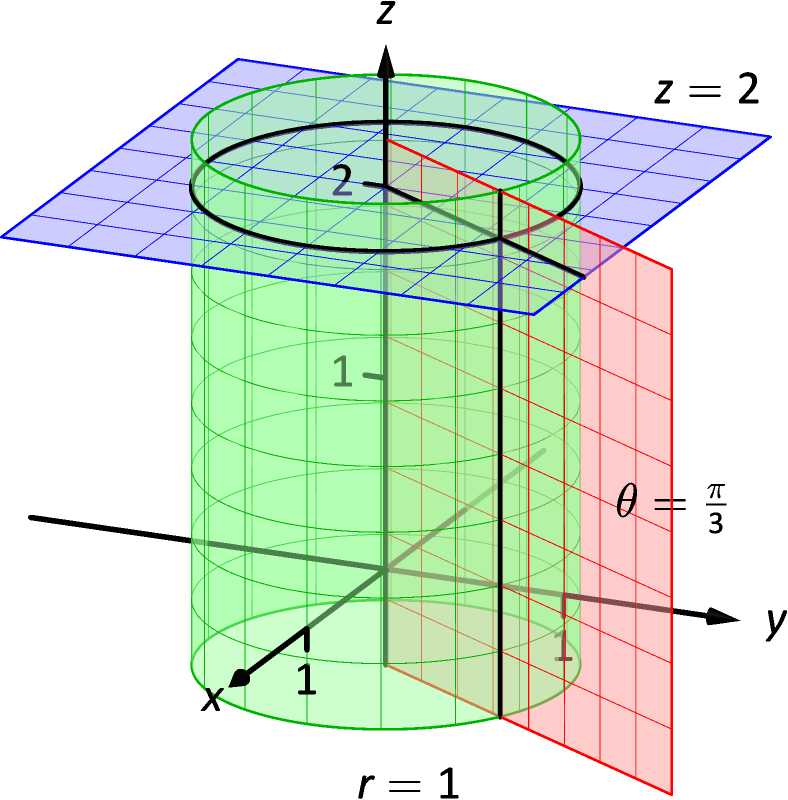



14 7 Triple Integration With Cylindrical And Spherical Coordinates Chapter 14 Multiple Integration Part Calculus Iii




4 Let E Be The Region In The First Octant Of R3 Contained In The Sphere A Formulate The Triple Integral Jj Jbzdv Jjje Zdrdydz In Spheri Iterated Integrals Ca Coordinates As




We Consider The Hemi Sphere X 2 Y 2 Z 2 16 And Chegg Com




Engineering Mathematics 233 Solutions Double And Triple Integrals




Finding Volume For Triple Integrals Using Spherical Coordinates Krista King Math Online Math Tutor




Graph The Cylinder X 2 Y 2 16 And The Sphere X 2 Y 2 Z 2 49 Together Using Maple And Find The Volume Outside The Cylinder And Inside The Sphere Study Com



Solved Use Cylindrical Coordinates Evaluate Iii




Section 9 1 Three Dimensional Coordinate Systems X 2 Y 2 Z Sx 2 Y 2 Z 2 2 Xy Plane It Is Sketched In Figure Pdf Free Download




Use Spherical Coordinates Evaluate Triple Chegg Com



Q Tbn And9gcraqjej478vyisyz3yjyvk Sihuo59aaiv7zoqlbbud6g1ghdeq Usqp Cau
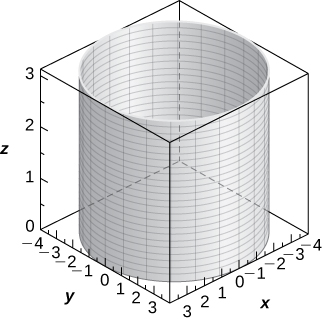



11 7e Exercises For Cylindrical And Spherical Coordinates Mathematics Libretexts



2
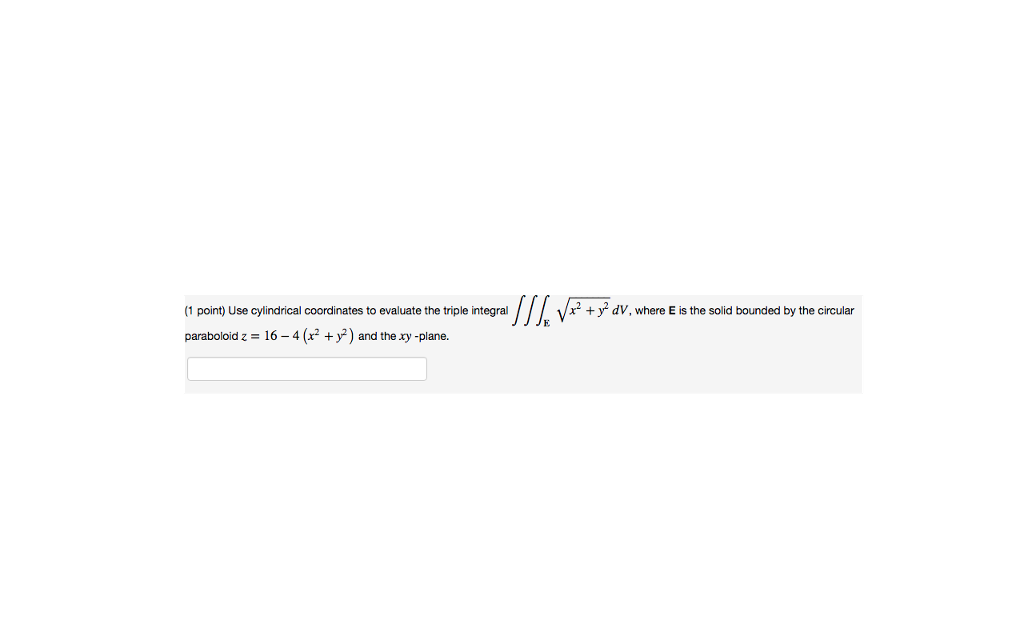



Use Cylindrical Coordinates To Evaluate The Triple Chegg Com




Hw13sol Pdf Version 001 Hw13 Not For Credit Perutz This Print Out Should Have 22 Questions Multiple Choice Questions May Continue On The Next Course Hero



Triple Integrals In Cylindrical And Spherical Coordinates




Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange




Write The Equation In Spherical Coordinates A X 2 Chegg Com



2



1




Cylindrical Coordinates In Matlab



The Divergence Theorem



Surface Area




Use Spherical Coordinates Evaluate Triple Chegg Com




Write The Equation X 2 Y 2 Z 2 16 Using Chegg Com




Write The Equation In Spherical Coordinates A X2 Chegg Com
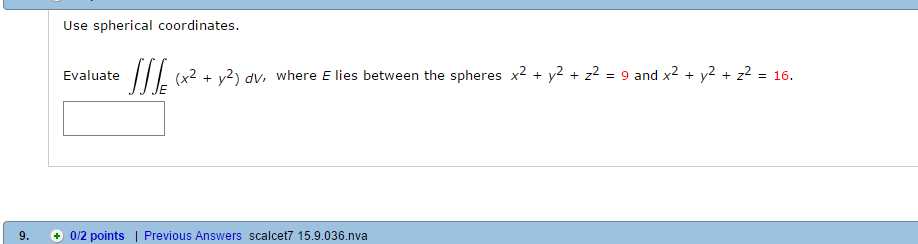



Use Spherical Coordinates Evaluate Triple Chegg Com



1



14 7 Triple Integration With Cylindrical And Spherical Coordinates Chapter 14 Multiple Integration Part Calculus Iii



2




Contiune On 16 7 Triple Integrals Figure 1 Ef X Y Z Dv




Triple Integrals In Spherical Coordinates Article Khan Academy



2



Calculation Of Volumes Using Triple Integrals Page 2
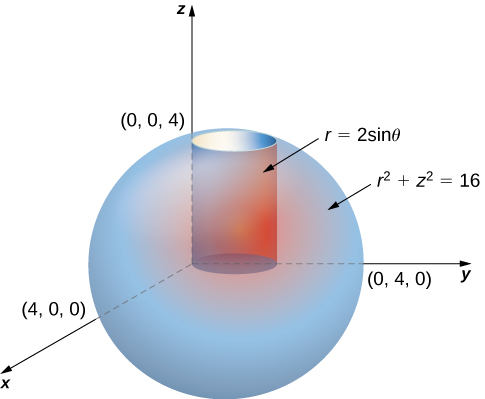



Triple Integrals In Cylindrical And Spherical Coordinates Calculus




Multiple Integrals H 2 Y Are Continuous Functions On C D And Let F X Y Be A Function Defined On R Then Pdf Free Download




Use Spherical Coordinates Find The Volume Of The Chegg Com



2
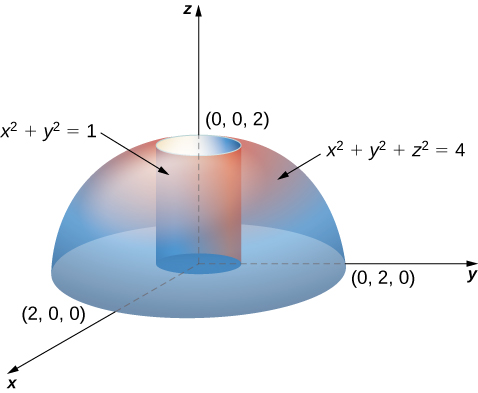



Triple Integrals In Cylindrical And Spherical Coordinates Calculus Volume 3




Document




In Spherical Coordinates For The Region X 2 Y 2 Z 2 Geq1 X 2 Y 2 Z 2 Leq4 Z Geq Sqrt X 2 Y 2 Why Does Psi Range From 0 To Pi 2 Mathematics Stack Exchange




15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts



Surface Area



Surfaces Part 3
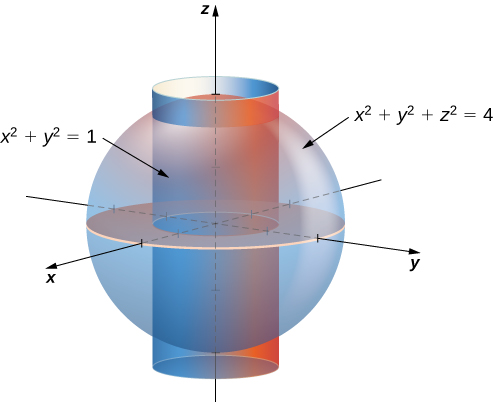



Triple Integrals In Cylindrical And Spherical Coordinates Calculus




Assignment Previewer




Chapter 16 Answer
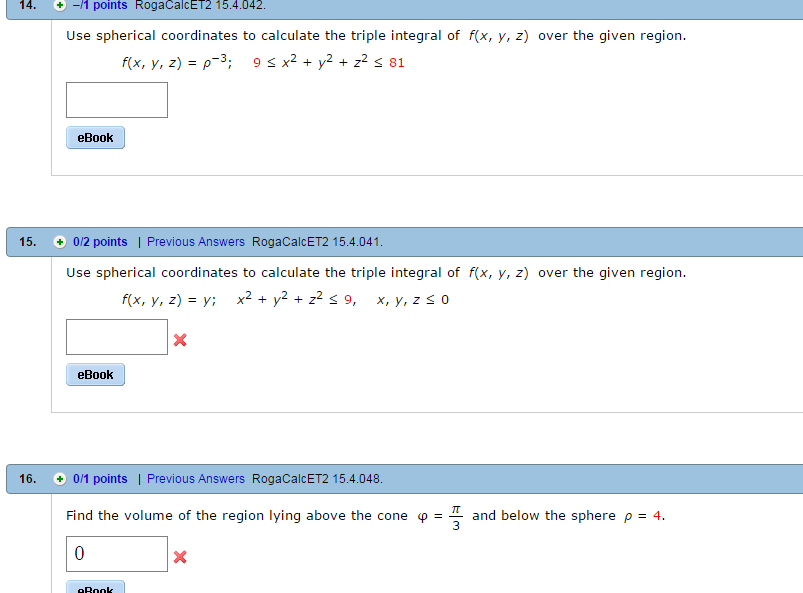



Use Spherical Coordinates To Calculate The Triple Chegg Com




Triple Integrals In Spherical And Cylindrical In Rectangular Coordinates Dv Dzdydx In Cylindrical Coordinates Dv R Dzdrd8 In Spherical Coordinates Ppt Download




14 7 Triple Integration With Cylindrical And Spherical Coordinates Chapter 14 Multiple Integration Part Calculus Iii
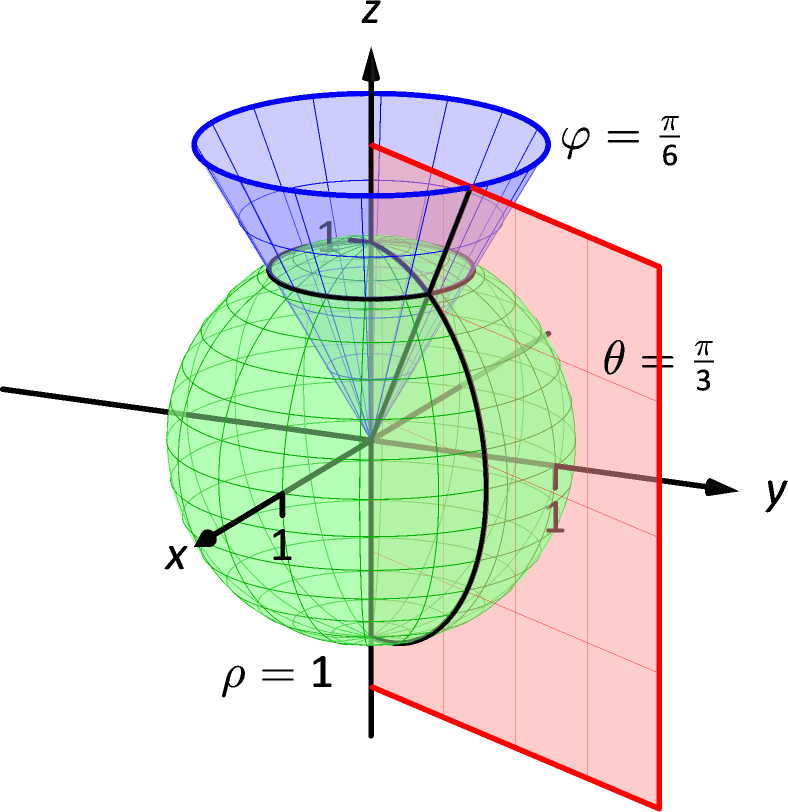



14 7 Triple Integration With Cylindrical And Spherical Coordinates Chapter 14 Multiple Integration Part Calculus Iii



2




Use Spherical Coordinates Evaluate Tripleintegral E Chegg Com




Find The Volume Of The Solid Inside Both X 2 Y 2 Z 2 A 2 And X A 2 2 Y 2 A 2 2 Using A Triple Integral On Cylindrical Coordinates Mathematics Stack Exchange




15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts




Consider The Solid Bounded Above By The Plane Z 4x And Below The Circle X 2 Y 2 16 In The Xy Plane A Write The Double Integral In Rectangular Coordinates To




1 Point Use Spherical Coordinates To Evaluate The Triple Integral Dv E X Y Z E Vx2 Y2 Homeworklib




5 12 Pts Evaluate The Following Triple Integral Where The Region E Lies Above The Cone 32 32 And Below The Sphere Y2 5 12 Pts Evaluate The Following Triple Integral Where The Region Homeworklib



2




Use Spherical Coordinates Evaluate Jilv Y Dv Chegg Com




Use Spherical Coordinates Evaluate The Triple Integral Over E Of Sqrt X 2 Y 2 Z 2 Dv Where E Lies Above The Cone Z Sqrt X 2 Y 2 And Between The Spheres X 2
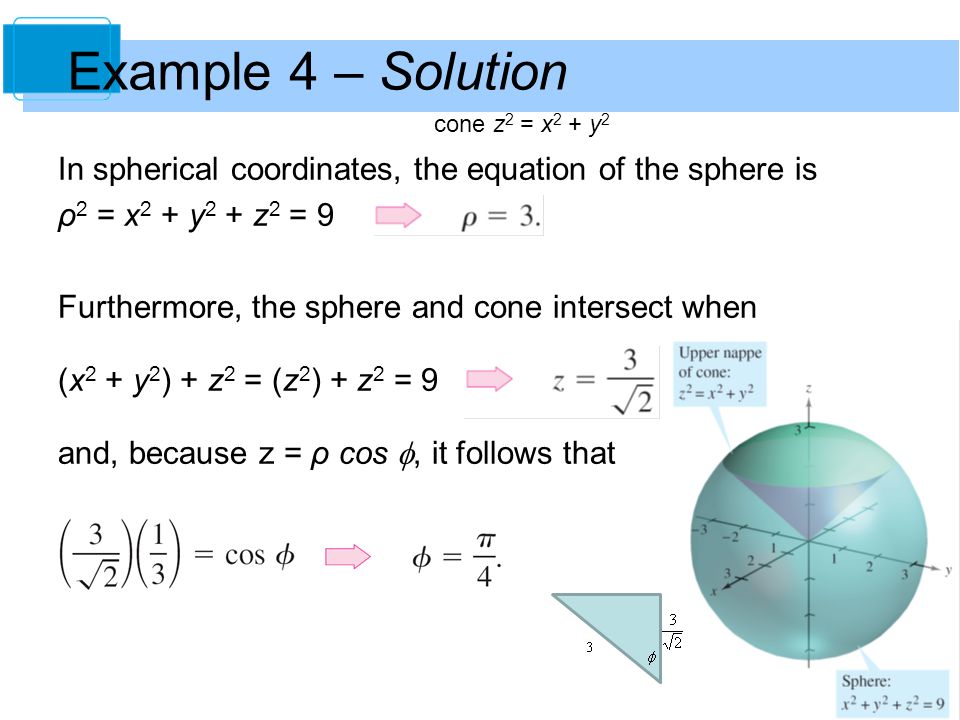



Multiple Integration 14 Copyright C Cengage Learning All Rights Reserved Ppt Download




Notes Up To Ch7 Sec3




Consider The Region Above The Xy Plane Inside The Sphere X 2 Y 2 Z 2 16 And Outside The Cylinder X 2 Y 2 4 A Sketch The Region B Use Polar Coordinates To Find The Volume



2
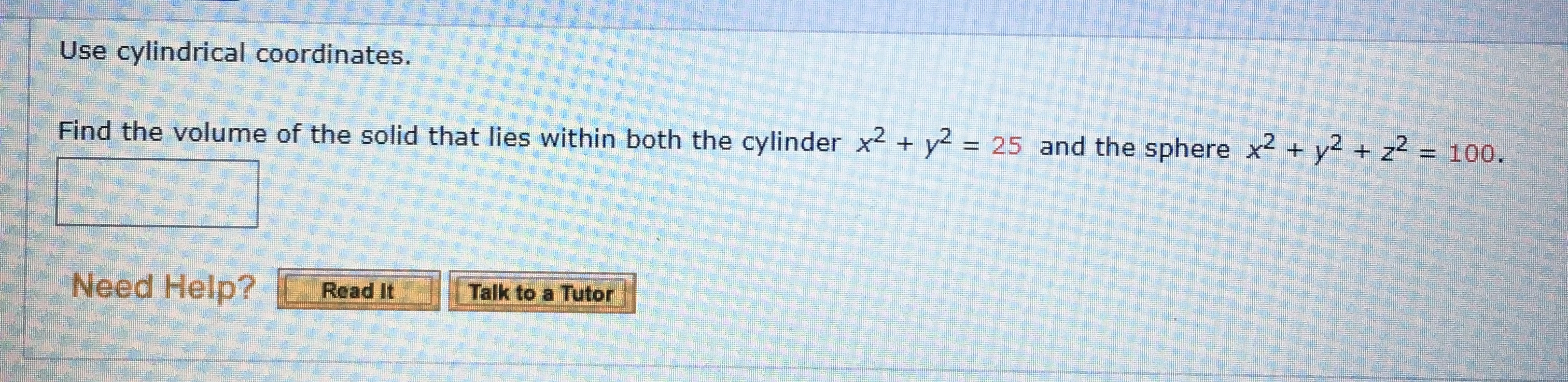



Answered Use Cylindrical Coordinates Find The Bartleby




Multivariable Calculus Surface Area Of Sphere X 2 Y 2 Z 2 16z Within Paraboloid Z X 2 Y 2 Mathematics Stack Exchange




Write The Equation In Spherical Coordinates X 2 Chegg Com



2




Volume Of A Snow Cone In Cylindrical And Spherical Coordinates Youtube




Functions And Planes Cylindrical Spherical And Polar Coordinates




Functions And Planes Cylindrical Spherical And Polar Coordinates
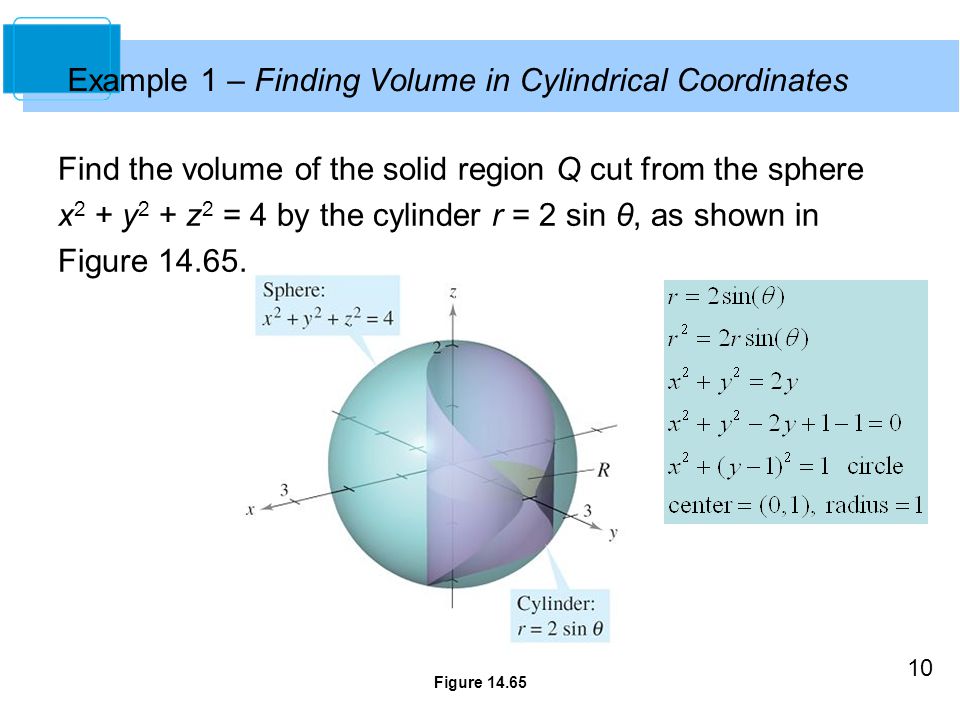



Multiple Integration 14 Copyright C Cengage Learning All Rights Reserved Ppt Download




Use Cylindrical Coordinates To Find The Volume Of The Solid Enclosed By The Cylinder X 2 Y 2 9 Text And The Sphere X 2 Y 2 Z 2 16 Study Com
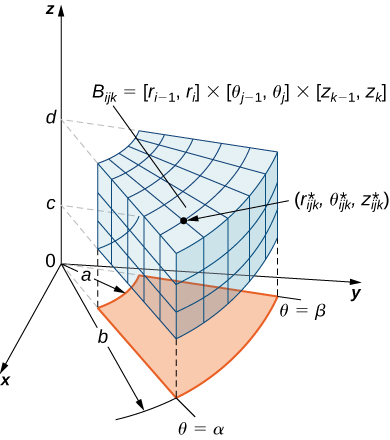



15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts



2
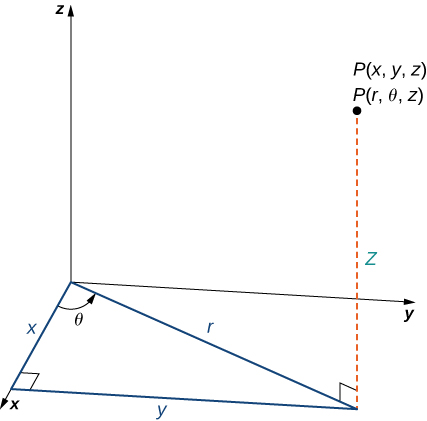



Cylindrical And Spherical Coordinates Calculus Volume 3
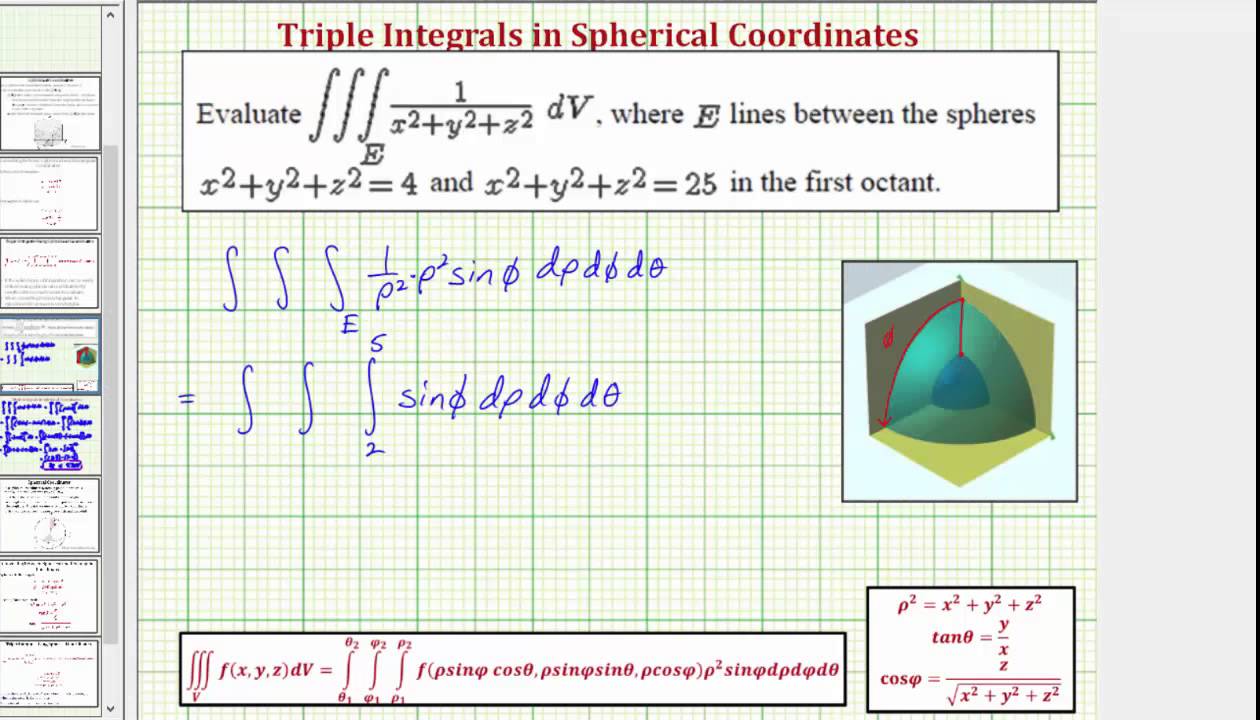



Evaluate A Triple Integral Using Spherical Coordinates Triple Integral Of 1 X 2 Y 2 Z 2 Youtube



Polar Html



0 件のコメント:
コメントを投稿