いろいろ 30 60 90 üçgeni soruları 404141

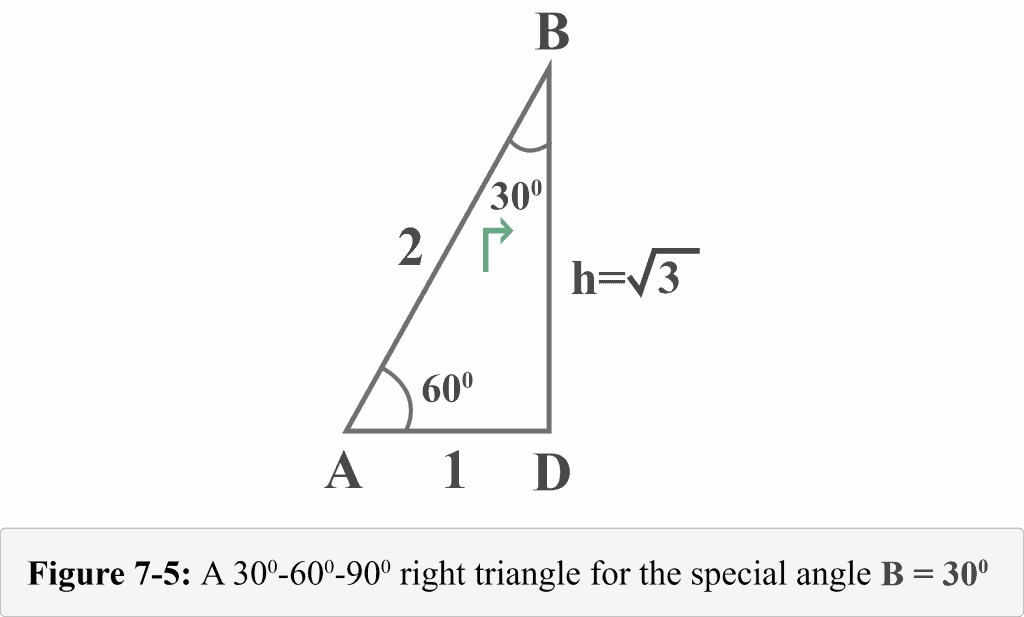
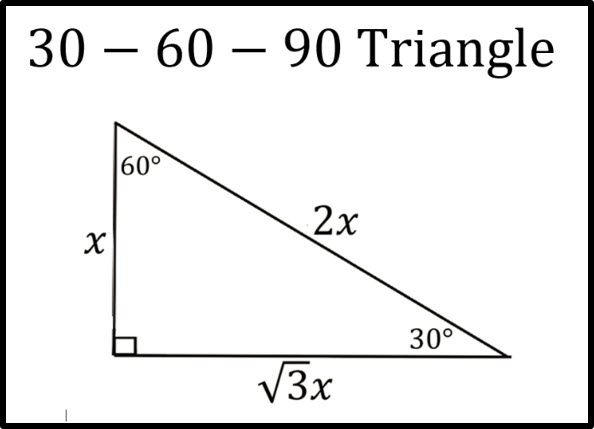
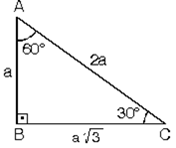
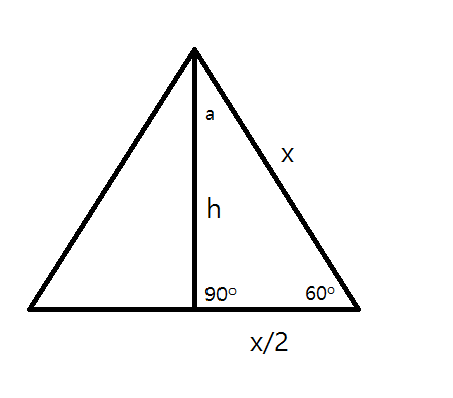
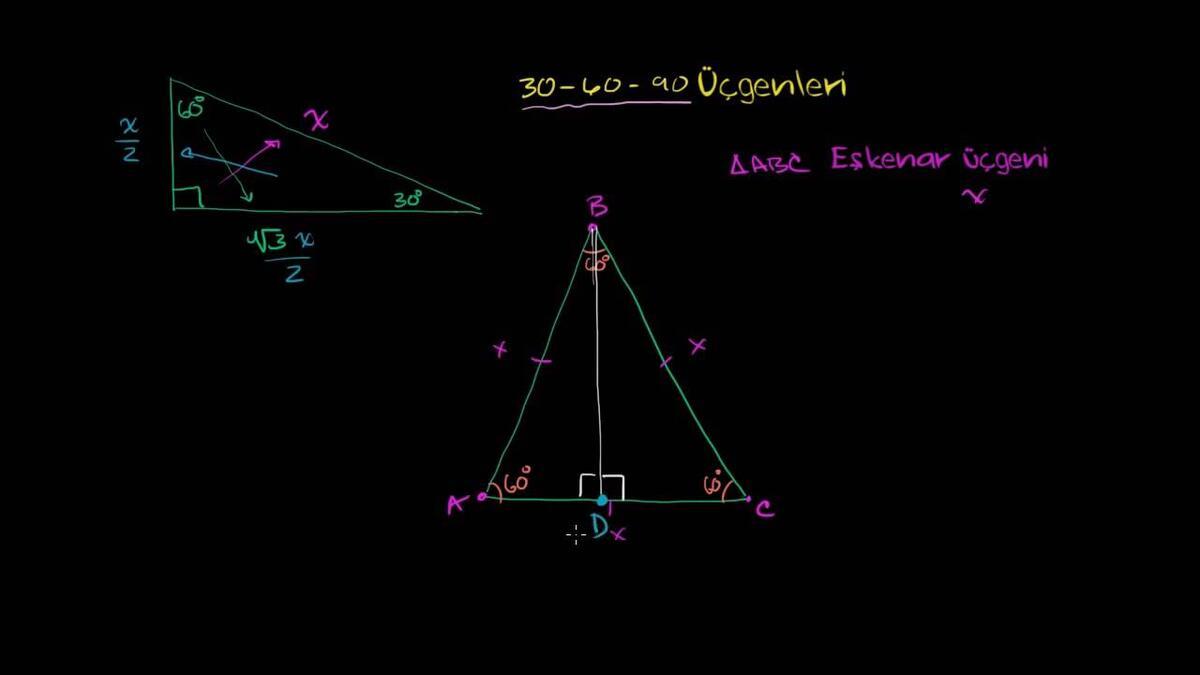
30°'nin karşısındaki kenarhipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki kenarın Ö3 katıdır 5 (30° – 30° – 1°) Üçgeni (30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik« 30 30 1 ÜÇgenİ 15 75 90 ÜÇGENİ → 9Sınıf Özel Üçgenler Konu Özeti ve Çözümlü Soruları sunusunun 45 45 90 ÜÇGENİ slaytını görüntülemektesiniz30 – 60 – 90 ÜÇgenİ Eşkenar üçgende bir kenara ait yükseklik çizilirse oluşan iki dik üçgenin de açıları 30° – 60° – 90° olur Bu eşkenar üçgenin bir kenarının uzunluğunu 2a kabul edersek, oluşan dik üçgenlerde 30 derecelik açının karşısı a olur çünkü yükseklik aynı zamanda kenarortaydır

Ikizkenar Ucgen Soru Cozumu Matematik Kitap Cozumleri Matematik Kalesi

30 60 90 üçgeni soruları

30 60 90 üçgeni soruları- 30 60 90 üçgeni 17 Temmuz 18 by ibrahimhocca , posted in Genel 30 60 90 üçgeni 30 60 90 üçgeni çoğu soruda karşımıza gelir o nedenle bu üçgenin özelliklerini iyi bilmek gerekir Olay çok basit öncelikle dik üçgeni tanıyalım Dik üçgen olması için zaten üçgenin açılarından biri 90 derece olmalıEşkenar Üçgen Konu Anlatımı Üç kenarı birbirine eş ve iç açılarının her birinin ölçüsü 60°'dirHerhangi bir yükseklik eşkenar üçgeni iki tane üçgenine ayırırEşkenar üçgenin yükseklikleri, açıortayları ve kenarortayları eşittir Şimdi Eşkenar üçgenlerle ilgili bilmen

Understanding 30 60 90 Triangles High School Math

Yukarıda da belirttiğimiz gibi özel üçgenler geometri için çok önemlidir Bu nedenle sadece 45 45 90 şeklinde değil de birçok farklı konuda bu üçgen karşımıza çıkabilir 30 60 90 üçgeni Geometrinin açılar konusunun belirli kurallara bağlı olan özel üçgenlerinden birisidir 30 60 90 üçgeni özelliklerinin bilinmesi geometrinin temel kurallarındandır Geometri dersi bir bisikletin zinciri gibidir Dişlisinden birisi dahi çıkan bisiklet zinciri tamamen işlevini yitirdiği gibi geometri de öyledirDaha fazlası için http//wwwkhanacademyorgtrMatematikten sanat tarihine, ekonomiden fen bilimlerine, basit toplamadan diferansiyel denklemlere, ilkokul s

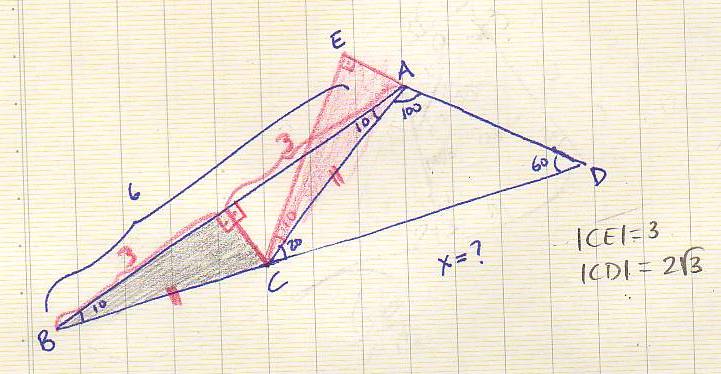
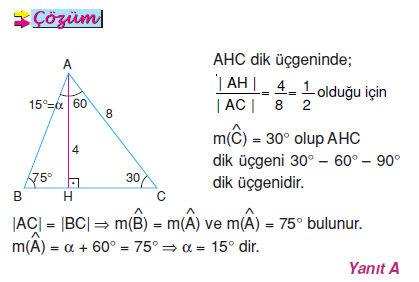
 İlgili yazı 30 60 90 üçgeni 45 45 90 Üçgeni Soruları Nasıl Çözülür? 45 45 90 üçgeni ile 30 60 90 üçgeni arasında ilişki kurmak için bazı sorularda bu iki üçgen iç içe verilebilir Yukarıdaki örnekte olduğu gibi bu tür sorularda bazen çizim yöntemini kullanarak iki üçgeni elde etmemiz gerekir30 8 3 60 30 60 6 4 Şekildeki diğer açılar bulunur ABC ve CDE (30 60 90 ) üçgenidir ABC üçgeninde 30 nin karşısındaki kenar AB = 3 br ise hipotenüsün uzunluğu BC = 6 br dir CDE üçgeninde, 30 nin karşısı hipotenüsün yarısı ise CD = 4 br dir Buradan BD = 6 4 = 10 br olur Cevap D'dir m(BAC) = 105

5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur30 60 90 üçgeni soruları, 45 45 90 üçgeni ile ilgili sorular, 15 75 90 üçgeni soruları, diklik merkezi soruları, muhteşem üçlü soruları, özel üçgen soru, pisagor bağıntısı soruları, 30 60 90 üçgeni çözümlü sorular, diklik merkezi soru çözümü, 15 75 90 üçgeni soru çözümü, pisagor çözümlü sorular30°'nin karşısındaki kenarhipotenüsün yarısına eşittir 60° nin karşısındaki kenar,30° nin karşısındaki kenarın Ö3 katıdır 5 (30° – 30° – 1°) Üçgeni (30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik

Special Angles In Trigonometry

Trigonometry Review With Ib Diploma Questions Ck 12 Foundation

Refleks 4 15°– 75°– 90° Üçgeni Refleks 7 Şerit Çubuk Soruları 655; 30 60 90 üçgeni ile ilgili soruları zaten çoğunlukla bu şekilde görürüz Yani karşımıza üçgeni çıkarıp bize basit soru sormazlar Bunu elde etmemizi isterler 45 45 90 üçgeni ile 30 60 90 üçgeni arasında ilişki kurmak için bazı sorularda bu iki üçgen iç içe verilebilir Yukarıdaki örnekte olduğu gibi bu tür sorularda bazen çizim yöntemini kullanarak iki üçgeni elde etmemiz gerekir

8 Sinif Ozel Ucgenler 15 16

5 Soru 30 60 90 Ucgeni Youtube

Büyük üçgen 30 60 90 üçgeni olur 90 'nin karşısında 6 2 var sa 30 nin karşısında yarısı olur 6 2 3 2 dir 2 45 45 90 üçgeninde 45 nin karşısında 3 2 var sa; İkizkenar üçgen hakkında bildiğiniz bütün özellikler, 30 30 1 üçgeninde de geçerlidir 30 30 1 üçgeninin en güzel yanlarından biri de, 1 derecelik geniş açıdan tabana doğru indirilen dikme iki adet 30 60 90 üçgeni vermesidir Böylece öğrenciler soruları daha iyiRefleks 2 30°– 60°– 90° Üçgeni 559;

Calculating The Area Of A Quadrilateral Gmat Math

Special Right Triangles Andymath Com

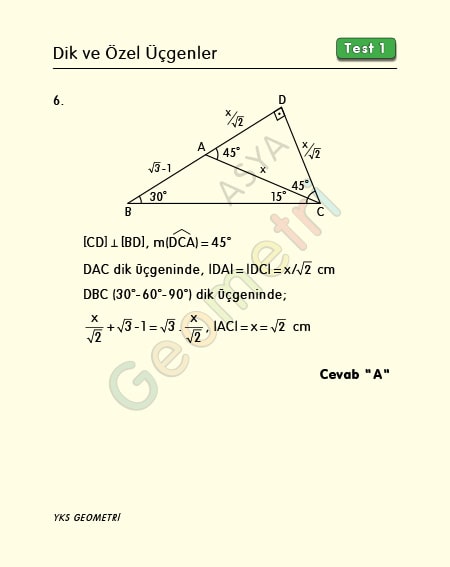
 (30° – 60° – 90°) dik üçgeninde; 30 60 90 Üçgeni 15 75 90 Üçgeni Özelliği Bu makaledeki notlar 15 75 90 üçgeninin özelliği 30 Özel Üçgenler Çözemediğiniz Geometri Soruları Hk Bu Bölüm Altında Çözemediğiniz Çözümünü Aradığınız GEOMETRİ Sorularını Sormanız İçin AçılmıştırBu ekitabın her hakkı saklıdır Tüm hakları Ali Selim YAMAN'a aittir Kısmen de olsa alıntı yapılamazMetin, biçim ve sorular elektronik , mekanik , fotokopi ya da herhangi bir kayıt sistemiyle çoğaltılamaz, yayımlanamaz

Dik Ve Ozel Ucgenler 1

Trigonometri Cikmis Sorular Ve Cozumleri Matematik Ogretmenleri

  üçgeni, üçgeni üçgeni ve eşkenar üçgen Bunları iyi bilirsek bazı soruları kalem oynatmaya gerek duymadan çözebiliriz ÖrGeometri konusundaki Üçgeni ile İlgili Soru başlıklı ders videosuna buradan ulaşabilirsiniz Khan Academy Türkçe Herkese, her yerde, dünya standartlarında, ücretsiz eğitim Khan Academy kar amacı gütmeyen bir uluslararası öğrenme platformudurABE üçgeninde 30 ve 90 derece duruyor, burada o zaman bu karşıdaki açı da 60 derece olmalı Yani buradaki AEB açısı da 60 olmalı BCD üçgeninde de 30 derecemiz var, 90 derecemiz var 180'e tamamlamak için burası 60 derece olmalı Ve işte ilk 3060

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

30 60 90 Ucgeni

 Özel üçgenler çözümlü sorular , üçgeni , üçgeni , ygs lys kpss soru çözümü hazırlık üçgeni kenar uzunlukları bulma 30 derecenin karşısındaki kenarın uzunluğu2 ÜÇGENİ Katlama Soruları En Kısa Yol Resim Önizleme Kapat Bu uygulama ADVERTI tarafından geliştirilmiştir wwwadverticomtr Öğretmenlerinizin 'şuradan bir dikme indir', 'buradan bir çizgi çek' dediği yerler aslında üçgeni bulmanız içindir 30 60 90, 45 45 90, 30 30 1 gibi bir tane de 15 75 90 üçgeni vardır Gelin 15 75 90 üçgeni özellikleri nasılmış, hep birlikte öğrenelim 15 75 90 Üçgeni Özellikleri

Net Fikir

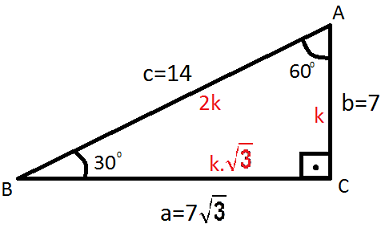
Ozel Ucgenler Cozumlu Sorular Bymutlu Com

 30 60 90 üçgeni çoğu soruda karşımıza gelir o nedenle bu üçgenin özelliklerini iyi bilmek gerekir Olay çok basit öncelikle dik üçgeni tanıyalım Dik üçgen olması için zaten üçgenin açılarından biri 90 derece olmalıE)3√32 Çözüm D den BC ye indirilen dikme nin solunda 3060 90 özel üçgeni oluşur ( B açısı eşkenardan 60) BH 30 un karşısı 6 nın yarısı 3 olur DH = 3√3 olur DHC üçgenidir , ikizkenar dik üçgen HC = 3√3 olur x 6 = 3 3√3 ise Dik üçgen olan 30 60 90 üçgeninin hemen yanına 60 derece içinden 15 derece daha açı tamamlayarak bir doğru parçası çekerseniz üçgen genişler ve siz yine 15 75 90 üçgeni ortaya çıkartmış olursunuz

30 60 90 Ucgeni Matematik Geometri Ve Turkce Blogu Dgs Ales Kpss

30 60 90 Ucgeni Ibrahim Hocca

30 60 90 üçgeni gibi bir çok kuralı bilen bir öğrenciler sınavlarda hem daha seri hem de oldukça başarılı olurla ve bir çok soruyu sıkılmadan kısa sürede çözebilirler Geometride karşımıza çıkan özel dik üçgenler bulunmaktadır Bu özel dik üçgenlerden bir tanesi ise 30 60 90 üçgenidir Bu 30 60 90 üçgeni bir eş üçgenin yükseklik ile iki eş parçaya bölünmesinden oluşmuştur Bu üçgenin açıları 30 derece 60 derece ve 90 derecedir Bu açıları gören kenarların uzunluklarının ise belirli bir kuralı bulunmaktadır 30 derecelikBazı dar açıların trigonometrik değerleri aşağıda verilmiştir Bu değerlerin çok iyi bilinmesi soruları daha hızlı çözmenizi sağlar 30 – 60 – 90 Üçgeni 45 – 45 – 90 Üçgeni 30 – 1 – 30 Üçgeni 15 – 75 – 90 Üçgeni Örnek1 Aşağıdaki ABC dik üçgeninde AB = 5 cm AC = 4 cm

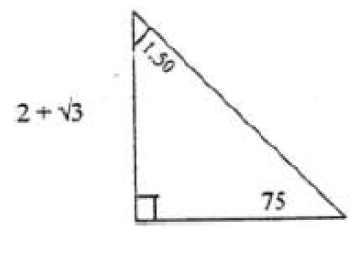
Given That Tan 75 0 2 Sqrt3 Find Without Using Tables Tan 15 0 In The Form P Qsqrtm Tutorke

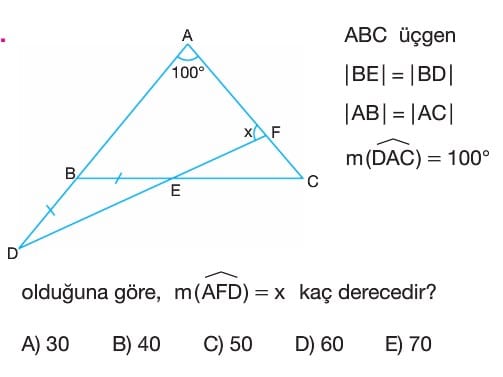
Ucgende Acilar Test Sorulari Cozumleri 9 Sinif Tyt Matematik

Bu yazımızda 30 60 90 Üçgeni, 45 45 90 Üçgeni, 30 30 1 Üçgeni, 15 75 90 Üçgeni, Üçgende İç Açılar Toplamı, Dış Açılar Toplamı, Roket Kuralı ve çok daha fazlası hakkında bilmen gerekenler ile Üçgende Açılar konusuna ait soruları çözerken işine yarayacağını düşündüğümüz ipuçları yer alıyor Umarız15 75 90 üçgeni 30 60 90 üçgeni 37 53 90 üçgeni  Üçgeni Bir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısında eşittir 60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın katına eşittir Bu yazıda 15 75 90 üçgeni kenar bağıntıları ve özellikleri üzerinde kısaca durmaya çalışacağız Geometri dersinde özel üçgenleri iyi bildiğimiz zaman geri kalan üçgenleri de bu üçgenlere benzeterek soruları çözme yoluna gideriz Daha önce 30 60 90 üçgeni yazısında başka bir temel üçgenin özelliklerinden

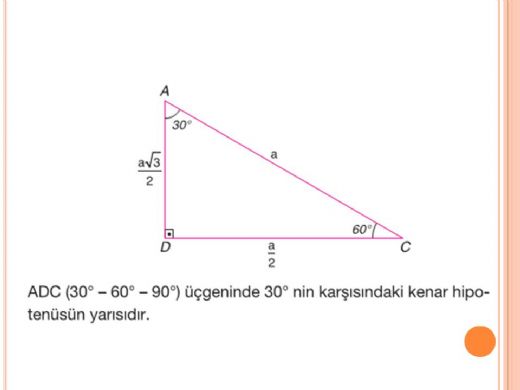
30 60 90 Ucgeni Pisagormatik

Senabil 9 Sinif Matematik Soru Bankasi Page 276 277 Created With Publitas Com

 C1 MGF üçgeni çıktı Daha sonra öklitten x'i bulursunuz 11 Ara 12 2337 #5 2337 #5 CEVAPLAR Dik indirebiliyor musun ona bak Eğer indirebiliyorsan üçgeni ya da üçgenini elde edebilirsin bu da soruları kısa yoldan çözmene yardımcı olabilirSinüs ve ister cos teoremi yazarsın istersen de B den AC ye dik inersin , dikme bir üçgeni oluşturur ve dikin uzunluğu 3√3 bulunur büyük üçgende pisagor yazılırsa (3√3)²(3AC)²=(√91)²

What Is A 30 60 90 Triangle Please Give An Example Socratic

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

 Özel üçgenler çözümlü sorular , üçgeni , üçgeni , ygs lys kpss soru çözümü hazırlık üçgeni kenar uzunlukları bulma –30 derecenin karşısındaki kenarın uzunluğuRefleks 8 Büyük Dikdörtgenleri Küçük 15 75 90 üçgeninin kenar uzunlukları (30° – 30° – 1°) Üçgeni (30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindeüçgeni Bu üçgende 15°'lik açının karşısındaki

Ikizkenar Ucgen Soru Cozumu Matematik Kitap Cozumleri Matematik Kalesi

Triangles On Sat Math Geometry Strategies And Practice Problems

 (30° – 60° – 90°) dik üçgeninde; Trigonometri Çıkmış Sorular ve Çözümleri Trigonometri Çıkmış Sorular ve Çözümleri İle ilgli LYS, ÖSS, TYT, AYT, MAT2 sınavlarında çıkmış tüm soruların çözümlerini pdf formatında inceleyebilrisiniz Trigonometri konusu da genellikle 11 sınıf ve 12 sınıf derslerinde işlenmektedir Özel Üçgenler İkizkenar üçgen, eşkenar üçgen, dik üçgen, 345 üçgeni, üçgeni gibi özel üçgenleri duymuş olmalısınız Bu konuda

A 400 V Three Phase Motor With A Power Factor Of 0 7 Has An Output Of 3 2 Kw Calculate A The Line Current B The Power Input Of Motor Kva And C The

30 60 90 Right Triangles Read Geometry Ck 12 Foundation

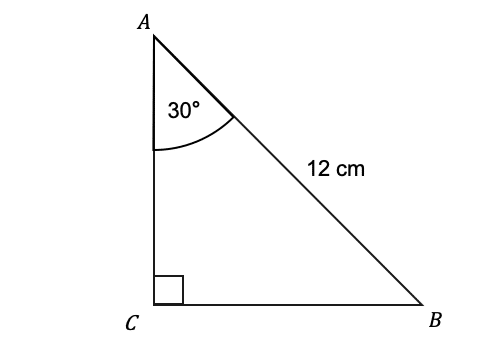
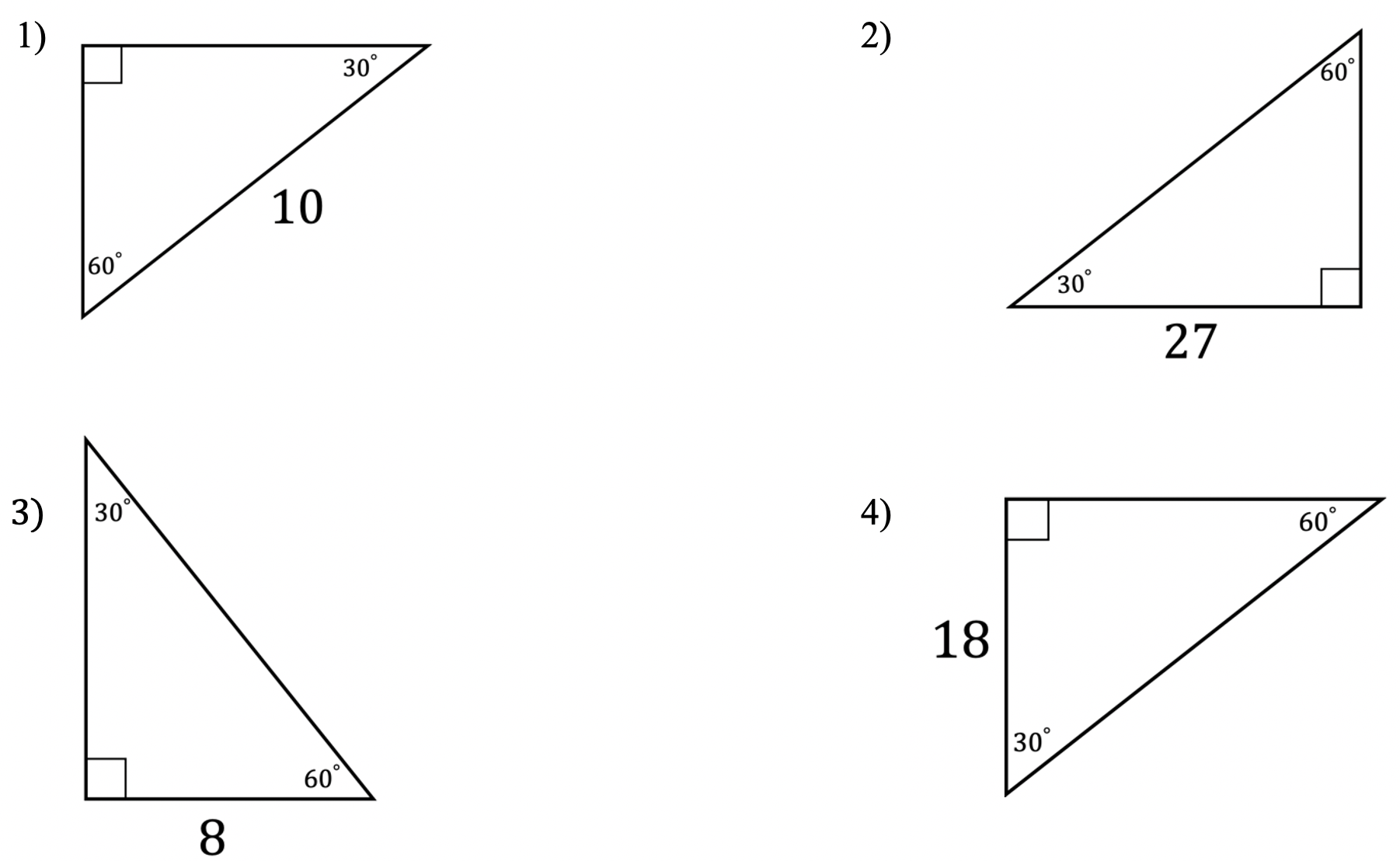
 30 60 90 ÜÇgenİ sorulari ABC bir dik üçgendir AB kenarı BC kenarına diktir m (BCA) = 30 derecedir AC kenarı uzunluğu ise 8 cm dir Bu verilere göre BC kenar uzunluğu kaç cm dir?Refleks 3 30°– 30°– 1° Üçgeni 432;

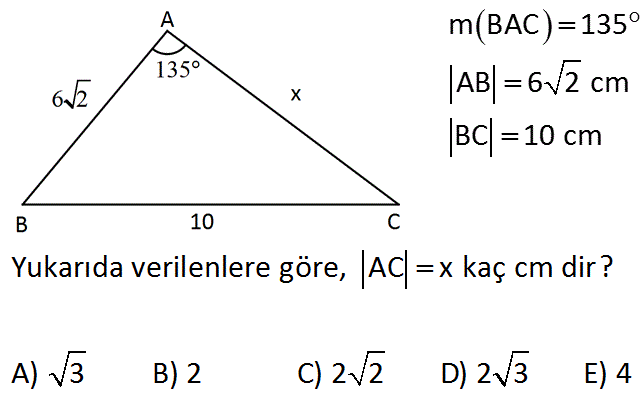
45 45 90 Ucgeni Ikizkenar Dik Ucgen

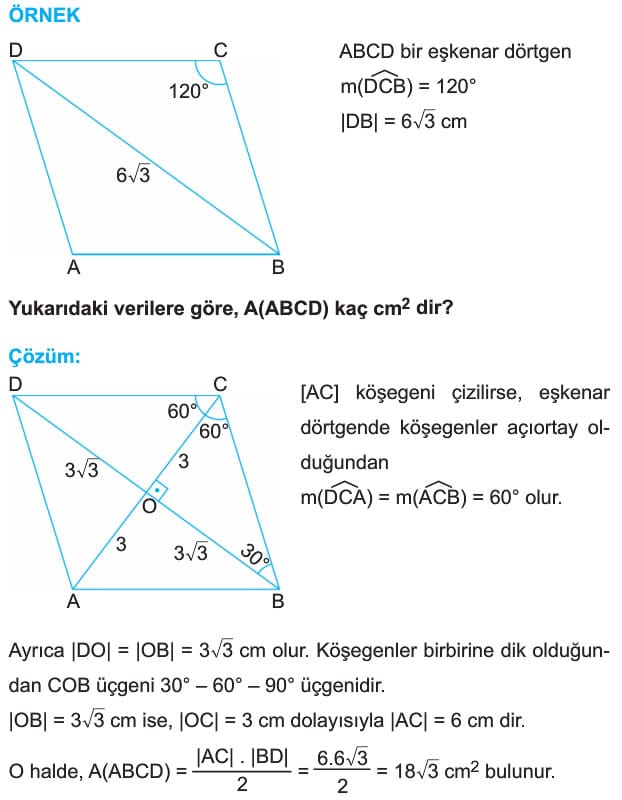
Eskenar Dortgen Ozellikleri Alani Sorulari Cozumleri Ornek 14

30 60 90 Ucgeni Ile Ilgili Soru Lutfen Cozumlu Olsun Eodev Com

En Hizli 30 60 90 Ucgeni Trigonometrik Oranlari Sorulari

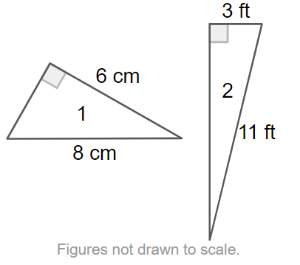
Missing Side Lengths Geogebra

30 60 90 Ozel Ucgenleri Ile Ilgili 10 Tane Cozumlu Soru Eodev Com

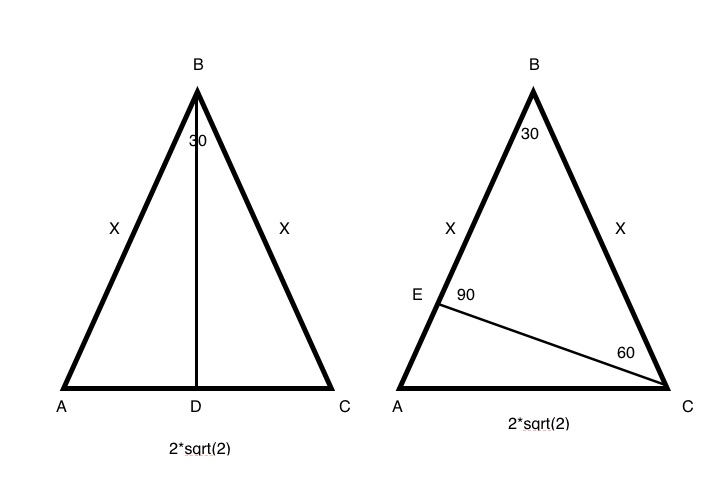
Angles And Arguments

Dik Ucgende 30 Un Karsisi 3 Ise 60 Ve 90 In Karsisi Ne Olur Eodev Com

Ucgenler Dik Ucgenler 4 30 60 90 Ucgeni Geometri Metin Hocam Youtube

Pythagorean Theorem Review 5 Questions If A Triangle

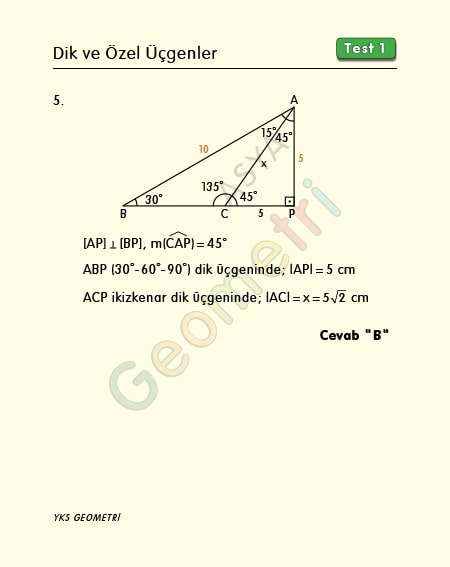
Vertical And Special Triangles Test 1

How To Find The Area Of An Equilateral Triangle Intermediate Geometry

Dik Ucgende Trigonometrik Oranlar

En Hizli 30 60 90 Ucgeni

Dik Ve Ozel Ucgenler Test 1

Dik Ucgende Trigonometrik Oranlar

Exam Style Questions On Construction Mensuration

45 45 90 Ucgeni Matematikce

Analyzing The Effects Of Particle Diameter In Cold Spraying Of Thermoplastic Polymers Springerlink

Solved Hello I Need Some Help With These Three Questions Chegg Com

30 60 90 Ucgeni Kurali Nedir 30 60 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri

30 60 90 Right Triangles Read Geometry Ck 12 Foundation

Ucgenler Dik Ucgenler 4 30 60 90 Ucgeni Geometri Metin Hocam Youtube

Special Right Triangles Examples Worked Solutions Videos Special Right Triangle Right Triangle Triangle Worksheet

Q8 Draw A Rough Sketch Of Two Lido

Slopes And Friction And On Point Of Slipping Teaching Resources

Karekok Cep Test Soru Bankasi Cozumleri

Vertical And Special Triangles Test 5

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

30 60 90 Ucgeni Ve Ozellikleri Not Bu

Understanding 30 60 90 Triangles High School Math

Ayrik Matematik Icin 15 Fikir Matematik Ayrik Matematik Temel Matematik

Radfordmathematics Com

Vertical And Special Triangles Test 2 Course Geometry

Geometri Sorusu Donanimhaber Forum

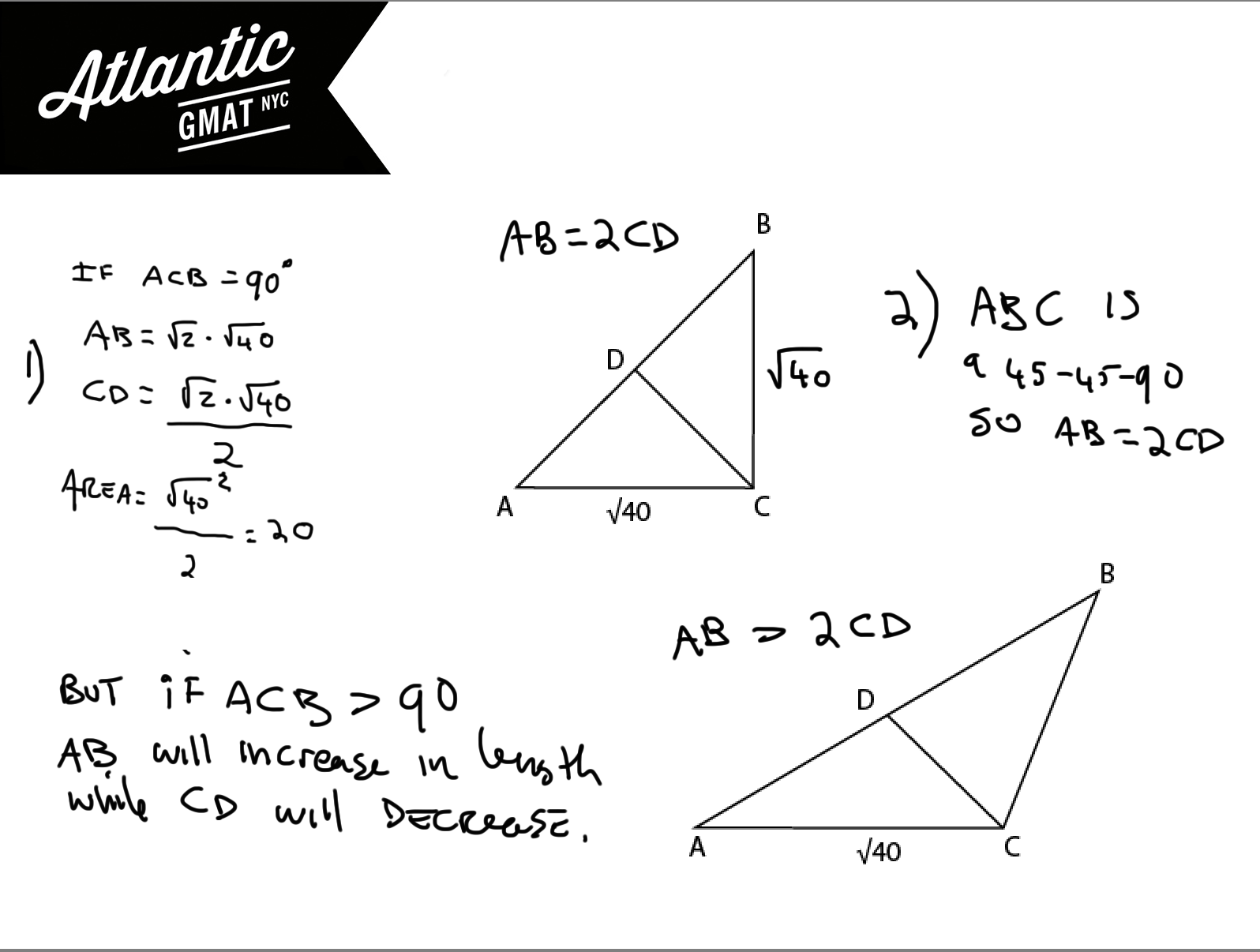
Gmat Question Of The Day Ds Geometry Gmat Tutor In Nyc Online

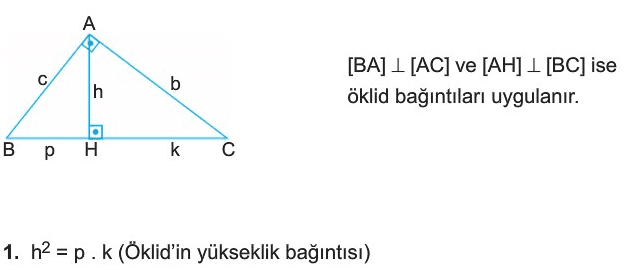
Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

How To Solve 30 60 90 Triangles Krista King Math Online Math Tutor

Geometri Soru Geometri Soru Paylasimi Ve Cozumu

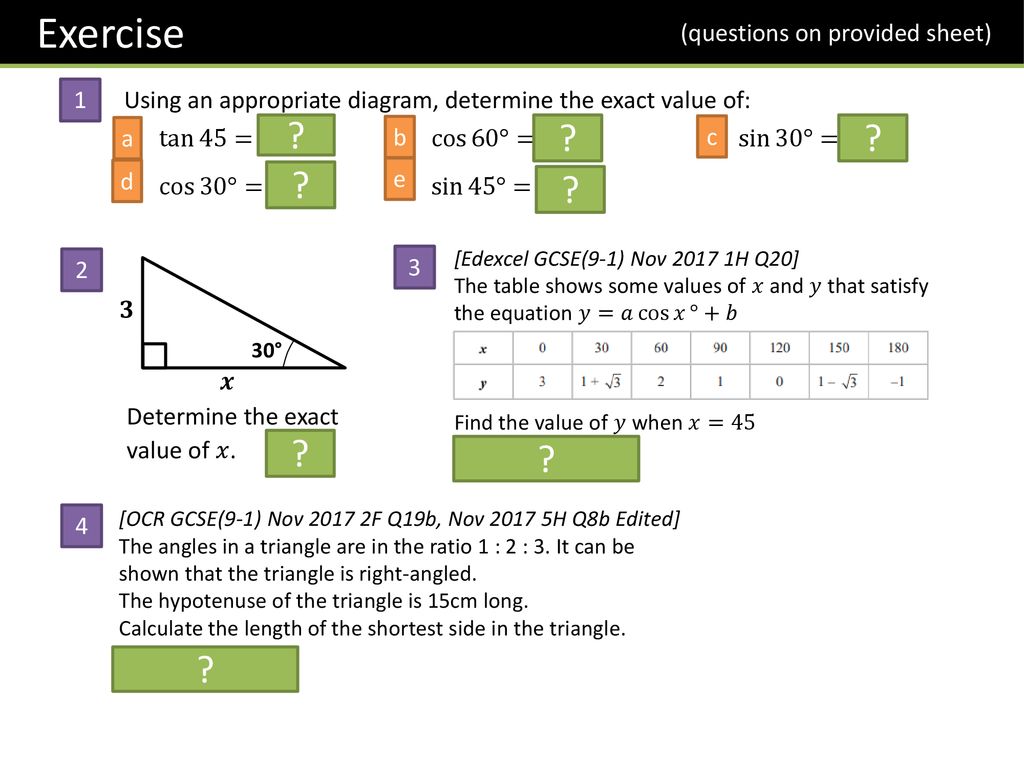
Gcse Exact Trigonometric Ratios Ppt Download

Worksheet 9a Part 2

Ikizkenar Eskenar Ucgen Sinav Sorulari

En Hizli 30 60 90 Ucgeni Kenar Bulma

30 60 90 Ucgeni Ile Ilgili Soru Geometri Trigonometri Youtube

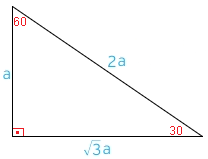
30 60 90 Ucgeni Webders Net

Body Example Reverse Png Triangle Rules Right Triangle Triangle

Compare Dispersing Light Into Colors With A Prism And With A Grating The 30 60 90 Triangle Prism Homeworklib

A Surveyor Toby Measures The Distance Between Two En Ya Guru

An Under Utilized Strategy For Gmat Geometry Questions Article Gmat

Solving Problems With Special Triangles Practice Algebra Practice Problems Study Com

Trigonometri 30 60 90 Ve 45 45 90 Ucgenleri Ile Trigonometrik Oranlari Youtube

Area Of A Triangle Using Angle Essential Questions

Pythagoras Identify The Hypotenuse Variation Theory

This Is A 30 60 90 Triangle What Is The Measure Of X 3 8 X X Sqrt Brainly Com

Test Special Right Triangles Terms Quizlet

Trigonometry Questions Worksheets And Questions Mme

30 60 90 Ucgeni Turleri Ve Ozellikleri

30 60 90 Right Triangles Read Geometry Ck 12 Foundation

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

File Applications Of Right Triangle Trigonometry Question 1 Svg Wikimedia Commons

Mat Geo Ders Aci Ozelucgenler Dikucgen Kalip Soru Cevap Cokonemli Denemetarzi Deneme Matematik Geometri Soru Ders Dersnotu Yks Ayt 19yks Sinav Not 19yks 19tayfa Facebook

30 60 90 Ucgeni Basit Bir Soru Yapabilirsiniz Eodev Com

Special Right Triangles 30 60 90 And 45 45 90 Triangles Matter Of Math

En Hizli 30 60 90 Ucgeni Kenar Bagintilari

Mathcounts Notes 14 Mathcounts State Prep Inscribed Circle Radius And Circumscribed Circle Radius Of An Equilateral Triangle

March30 April03

30 60 90 Special Triangle Archives Mathsux 2

30 60 90 Ucgeni Kurali Nedir 30 60 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Son Dakika Egitim Haberleri

How To Find The Perimeter Of A 30 60 90 Triangle Mathematics Stack Exchange

En Hizli Geometri 30 60 90 Ucgeni Ozellikleri

Bearing Capacity Of Strip Footings Adjacent To Anisotropic Slopes Using The Lower Bound Finite Element Method International Journal Of Geomechanics Vol No 11

8 Sinif Ozel Ucgenler 15 16

Do You Just Assume These Are 30 60 90 Triangles Sat

Special Angles In Trigonometry

The Shorter Leg Of A 30 60 90 Triangle Is 6 What Is The Length Of The Hypotenuse Socratic

Conquering Right Triangles The Pythagorean Theorem On Act Math Part 1 Magoosh Blog High School